本文章用于复习人工智能数学基础,题目基于老师的课件。主要是总结一些重要的题目案例,对于过于简单的例如行列式计算不作收录)内容由本人结合AI和ppt整合。可能会缺一定内容
为什么这门课这么难
线性代数部分
求解欠定线性方程组


1. 求 Ax = b 的一个特解
2. 求 Ax = 0 的所有解
3. 将前两步的解组合得到通解
(求齐次解的时候,先化成行阶梯最简型)右边无关变量竖排就能表示成原变量的组合
求解线性方程组


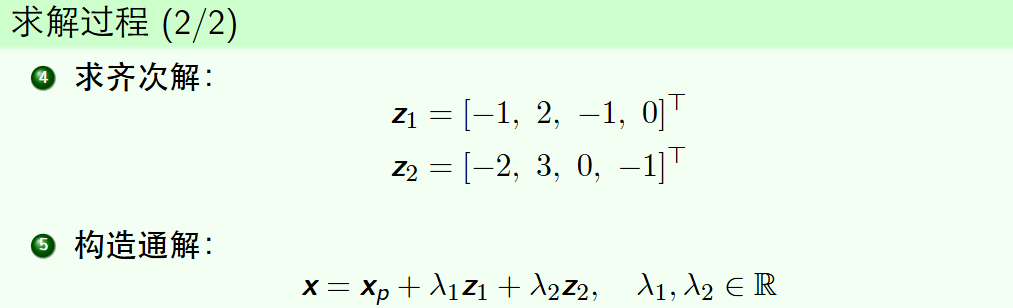
子空间判定



思路:
检查集合非空
检查加法律加法封闭(元素相加还存在)
检查乘法封闭
*第二题由于乘以负一后不存在于原来的集合所以不满足
张成的子空间

验证线性映射
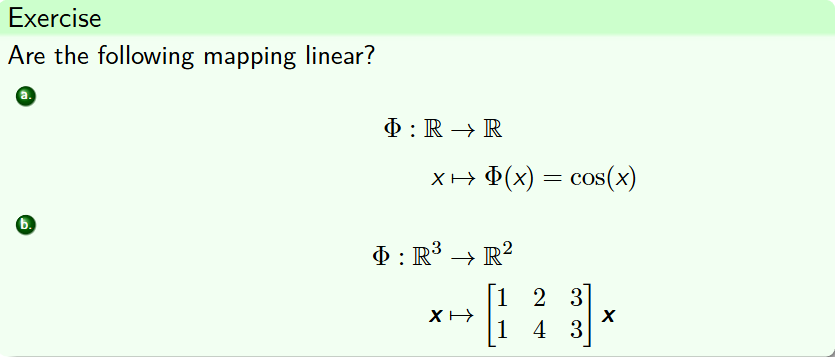
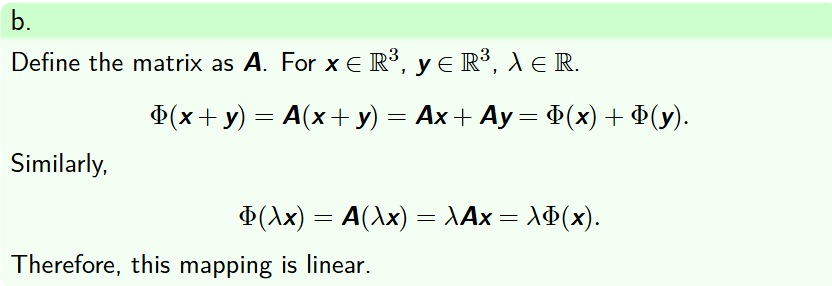
看加法乘法能否提取到外面
内积运算
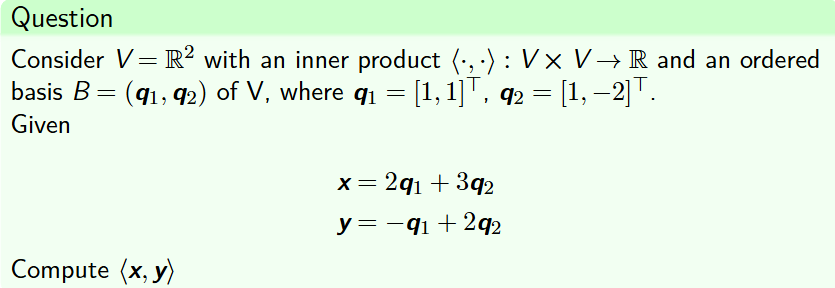
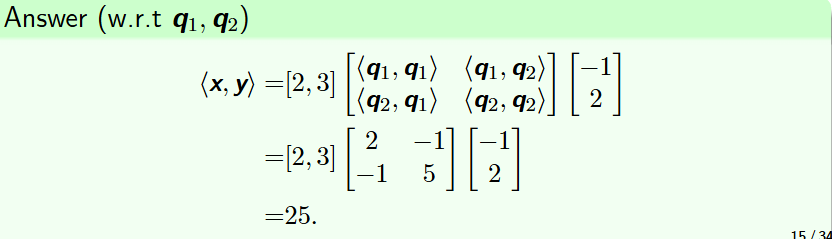
*也可以直接当做数乘运算来做
或者使用基底法

正定矩阵判断
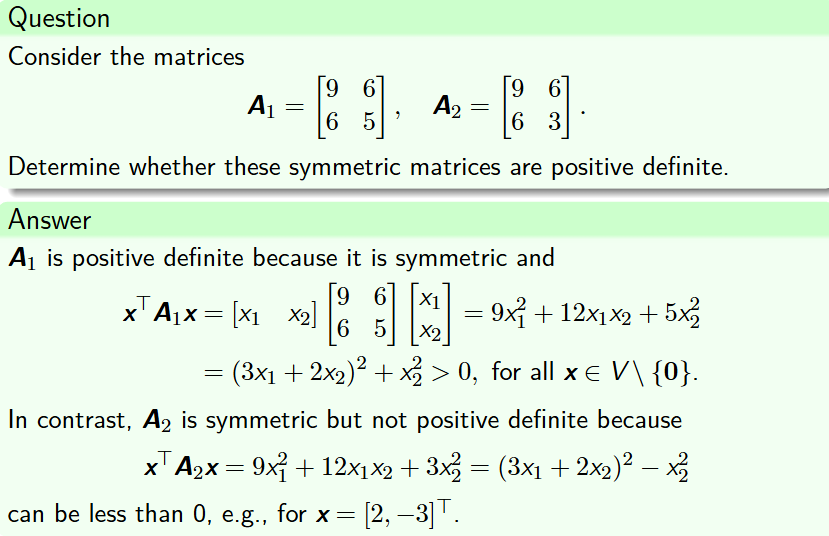
正定矩阵必须是对称矩阵,其次必须满足XTAX是大于零的。
向量距离

计算角度

正交投影(直线)
投影规则:

直观体现:
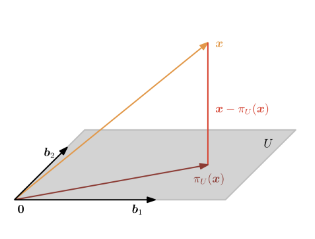
正交投影(一般形式)



行列式计算

计算特征多项式

特征多项式、特征值、特征空间


步骤:
计算det(A-λI) = 0
求解得出特征值
求出det(A-λI) X = 的解,得出对于λ所对应的span空间
特征分解与对角化


特征分解与对角化步骤:
计算特征值(求解det(A-λI))
计算Ap1 = λp1 对于所有λ的解
让所有解组合为一个新的矩阵,得到,计算A = PDP-1。其中D为对角矩阵,对角线上为特征值。
转置互相证明

技巧:变换特征向量,将v变为Av或者ATv
SVD奇异值分解

计算ATA

对ATA进行相似对角化,得到的 P就是奇异值分解中的V, 对D删掉只有零的行,将特征值降序排列求根号得到∑ 。
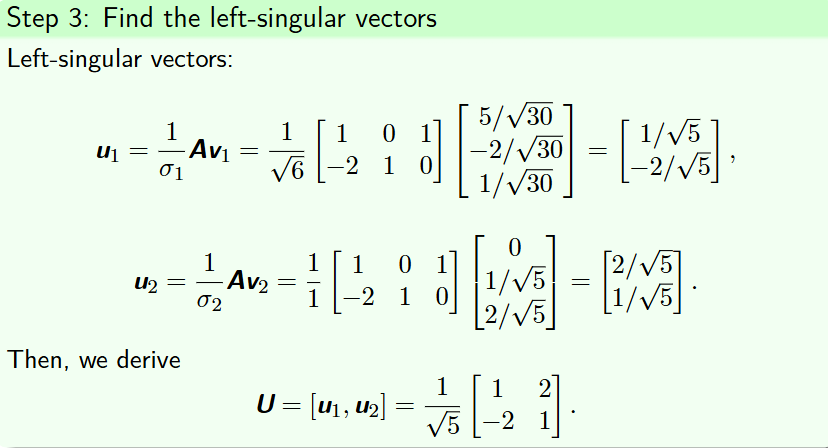
对V取竖行得到v1 v2, 计算1/σ * A * vn, 将得到的u进行品鉴
SVD最终形式为U∑VT
微积分部分
求泰勒多项式

泰勒多项式公式为:
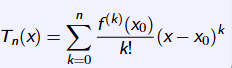
求函数导数
这个直接略了
求偏导数

无关变量视作常数,除非是变量的函数
求梯度

t是矩阵,tTt按照平方来求
向量视角求解链式法则

一般情形:

矩阵梯度计算
这里真的看不懂,略过了
概率论部分
概率分布计算

二项分布计算


图里的括号是组合数,相当于C102
边缘分布计算
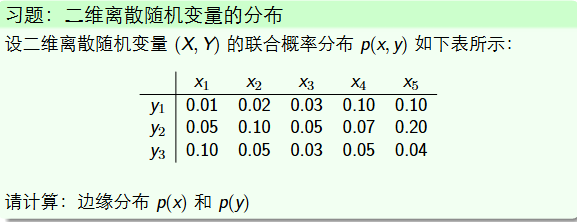

简单来说就是求单个变量分布
条件分布计算
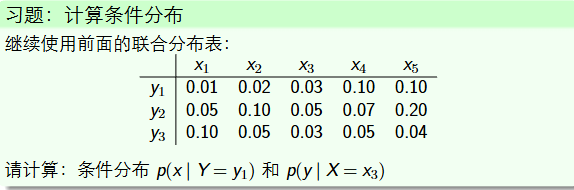

使用乘积规则:p(x, y) = p(x|y)p(y)
贝叶斯定理应用
贝叶斯公式:
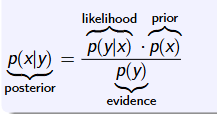
习题:



求数学期望
离散型

连续型(求积分)


求随机变量的方差


协方差计算

二项随机变量的期望与方差

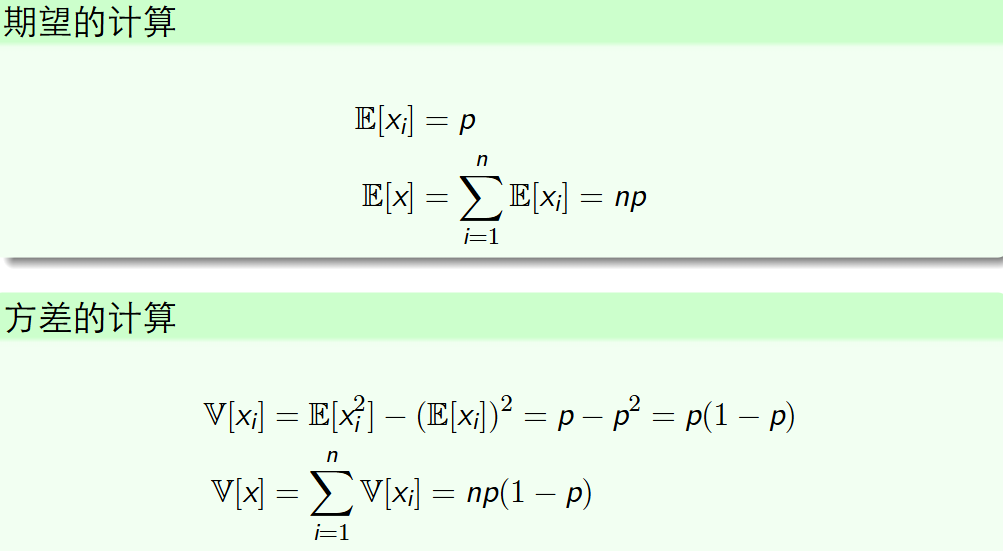
机器学习部分
求极点


手动计算梯度下降


思路:
计算梯度(求导)
计算x1 = x0 − γ∇f(x0)
重复计算
图解法求解方程
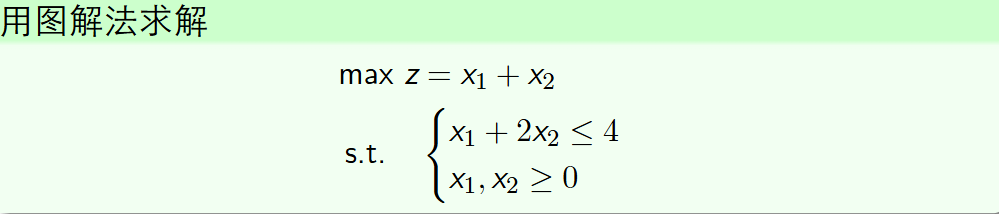
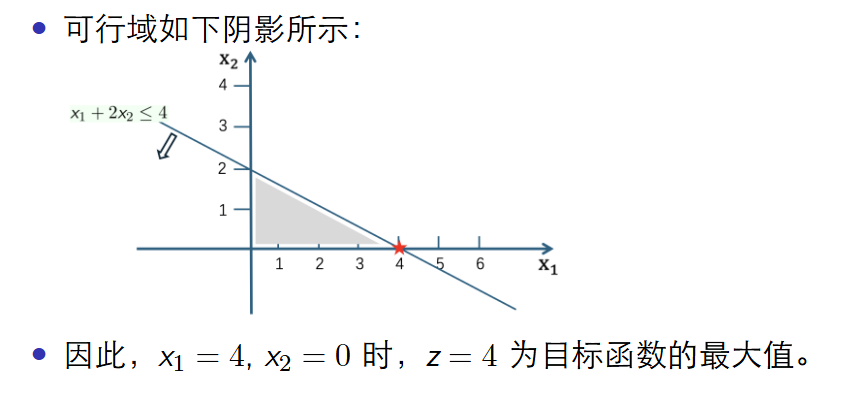
根据条件画图,求出条件中符合要求的点

